1 头文件
gsl_poly.h
2 多项式计算
$$P(x)=c[0]+c[1] x+c[2] x^{2}+\cdots+c[l e n-1] x^{l e n-1}$$
1
2
3
4
5
6
7
8
9
10
11
12
|
// gsl_poly.h
/* real polynomial, real x */
INLINE_DECL double gsl_poly_eval(const double c[], const int len, const double x);
/* real polynomial, complex x */
INLINE_DECL gsl_complex gsl_poly_complex_eval(const double c [], const int len, const gsl_complex z);
/* complex polynomial, complex x */
INLINE_DECL gsl_complex gsl_complex_poly_complex_eval(const gsl_complex c [], const int len, const gsl_complex z);
/* 计算多项式以及多项式的多阶导数,多阶导数的计算结果存在 res 数组中,从第 0 阶开始 */
int gsl_poly_eval_derivs(const double c[], const size_t lenc, const double x, double res[], const size_t lenres);
|
3 差商计算
差商基本介绍
-
差商如何计算?
给定 $n+1$ 个数据点(插值点),$(x_0, y_0),(x_2,y_2) \cdots(x_n,y_n)$,那么就可以计算差商了 。
-
差商有什么用?
构建多项式
比如构建牛顿多项式,其利用差商可以表示为:
$$N(x)=y_0+\sum_{j=1}^{n} [y_0,y_1,\cdots y_j] (x-x_0)(x-x_1)\cdots(x-x_{j-1})$$
可以看到,利用差商 $[y_0,y_1,\cdots y_j]$,插值点的 $x$ 坐标,就可以构造出一个牛顿多项式。
也可以通过差商来构建厄密特多项式。
比如,对 $n+1$ 个插值点 $(x_0, y_0),(x_2,y_2) \cdots(x_n,y_n)$,不仅插值多项式要过插值点,同时插值多项式也要满足一阶导数条件,利用差商,相应的厄密特多项式可以写为:
其中:$m_{2j}=m_{2j+1}=y_j,z_{2j}=z_{2j+1}=y_j$
总结一下:通过差商配合插值点的横坐标就可以构造出多项式了。其实就是多项式的差商表述形式。
差商计算函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
// gsl_poly.h
/*
dd 差商数组,x 插值点横坐标数值,y 插值点横坐标数组,size 插值点数
根据 x, y 计算差商储存在 dd 中
*/
int
gsl_poly_dd_init(double dd[], const double x[], const double y[],
size_t size);
/*
根据 dd, xa 构造的多项式,计算在点 x 处的值
内联(ifdef HAVE_INLINE)
*/
INLINE_DECL double
gsl_poly_dd_eval(const double dd[], const double xa[], const size_t size, const double x);
/*
c 泰勒系数,xp 泰勒展开点,w 为工作空间,长度为 size
根据 dd, x 构造的多项式在点 xp 进行泰勒展开,泰勒系数存在 c 中
*/
int
gsl_poly_dd_taylor(double c[], double xp,
const double dd[], const double x[], size_t size,
double w[]);
/*
z 厄密特(一阶导条件)插值多项式的等效插值点横坐标数组,dd 厄密特差商数组
dya 一阶导条件,长度为 size
根据插值点 xa, ya, 一阶导条件 dya,计算厄密特多项式的差商和等效插值点横坐标,存储在 dd 和 z 中
*/
int
gsl_poly_dd_hermite_init(double dd[], double z[], const double xa[], const double ya[],
const double dya[], const size_t size);
|
4 二次方程
$$a x^{2}+b x+c=0$$
1
2
3
4
|
// gsl_poly.h
/*计算实根,无根时,x0,x1 不变,一个根 x0, 两个根 x0, x1 升序*/
int gsl_poly_solve_quadratic(double a, double b, double c,
double * x0, double * x1);
|
$$a z^{2}+b z+c=0$$
1
2
3
4
5
|
// gsl_poly.h
/*一个根 z0, 两个根 z0, z1 升序,先按实部,再按虚部*/
int
gsl_poly_complex_solve_quadratic(double a, double b, double c,
gsl_complex * z0, gsl_complex * z1);
|
5 三次方程
1
2
3
4
5
6
7
8
|
// gsl_poly.h
int gsl_poly_solve_cubic(double a, double b, double c,
double * x0, double * x1, double * x2);
int
gsl_poly_complex_solve_cubic(double a, double b, double c,
gsl_complex * z0, gsl_complex * z1,
gsl_complex * z2);
|
6 一般多项式方程
使用迭代的方法寻根
工作空间
多项式复工作空间类
gsl_poly_complex_workspace
定义:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
// gsl_poly.h
typedef struct
{
size_t nc ;
double * matrix ;
}
gsl_poly_complex_workspace ;
// vcruntime.h
#ifdef _WIN64
typedef unsigned __int64 size_t;
typedef __int64 ptrdiff_t;
typedef __int64 intptr_t;
#else
typedef unsigned int size_t;
typedef int ptrdiff_t;
typedef int intptr_t;
#endif
|
多项式复工作空间 分配和清理
1
2
3
4
5
6
7
|
// gsl_poly.h
// n 多项式的系数个数
// 返回一个工作空间指针
gsl_poly_complex_workspace * gsl_poly_complex_workspace_alloc(size_t n);
// 清理工作空间,根据工作空间指针 w
void gsl_poly_complex_workspace_free(gsl_poly_complex_workspace * w);
|
求解
$$P(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n-1} x^{n-1}$$
1
2
3
4
5
6
7
8
9
10
11
12
13
|
// gsl_poly.h
/*
n 系数数组长度,最高阶系数要求非0
将 n-1 个复根,存在 z 中, z 为 double 指针,指向长度为 2n-2 的数组
如果找到根,返回 GSL_SUCCESS
*/
int
gsl_poly_complex_solve (const double * a, size_t n,
gsl_poly_complex_workspace * w,
gsl_complex_packed_ptr z);
// gsl_complex.h
typedef double * gsl_complex_packed_ptr ;
|
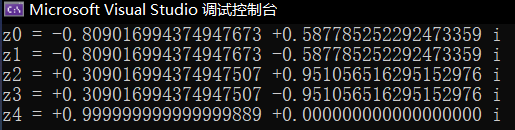
程序实例
计算:$P(x)=x^{5}-1$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
#include <stdio.h>
#include <gsl/gsl_poly.h>
int
main(void)
{
int i;
/* coefficients of P(x) = -1 + x^5 */
double a[6] = { -1, 0, 0, 0, 0, 1 };
double z[10]; // 因为是复根,所以是 2x5=10
gsl_poly_complex_workspace* w
= gsl_poly_complex_workspace_alloc(6);
gsl_poly_complex_solve(a, 6, w, z);
gsl_poly_complex_workspace_free(w);
for (i = 0; i < 5; i++)
{
printf("z%d = %+.18f %+.18f i\n",
i, z[2 * i], z[2 * i + 1]);
}
return 0;
}
|

7 引用和参考
https://www.gnu.org/software/gsl/doc/html/poly.html