1 用法,结果类,模式
用法
- 正常调用,返回计算值
- 错误句柄形式调用,返回错误码
以 $0$ 阶第一类贝塞尔函数 $J_0(x)$ 计算为例说明:
正常调用:
1
|
double y = gsl_sf_bessel_J0(x);
|
错误句柄形式调用:
1
2
|
gsl_sf_result result;
int status = gsl_sf_bessel_J0_e(x, &result);
|
结果类
这里的 gsl_sf_result 类定义:
1
2
3
4
5
6
|
// gsl_sf_result.h
struct gsl_sf_result_struct {
double val;
double err;
};
typedef struct gsl_sf_result_struct gsl_sf_result;
|
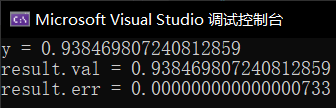
上述示例结果如下:

当结果溢出时,为了将结果保存,可以使用指数缩放。使用 gsl_sf_result_e10,定义为:
1
2
3
4
5
6
7
|
// gsl_sf_result.h
struct gsl_sf_result_e10_struct {
double val;
double err;
int e10;
};
typedef struct gsl_sf_result_e10_struct gsl_sf_result_e10;
|
这样,实际结果相应地变为 result.val * 10^(result.e10)
模式
gsl_mode_t: 模式类,用来控制精度,改变计算性能
定义:
1
2
3
4
5
6
7
|
// gsl_mode.h
// gsl_mode_t 就是个无符号整型
typedef unsigned int gsl_mode_t;
// 0,1,2 对应不同的精度
#define GSL_PREC_DOUBLE 0 // 相对精度大约是 2 x 10^(-16)
#define GSL_PREC_SINGLE 1 // 相对精度大约是 2 x 10^(-7)
#define GSL_PREC_APPROX 2 // 相对精度大约是 5 x 10^(-4)
|
2 参考
https://www.gnu.org/software/gsl/doc/html/specfunc.htm